Wrapped Addition
This post is part of a course on geometric modeling at the Summer Liberal Arts Institute for Computer Science held at Carleton College in 2021.
What time will it be 5 hours from now? What day is 10 days from now? As you work out the answers to these questions, you may find yourself incrementing a counter that wraps back around to the beginning when it reaches some maximum value. This practice of wrapping is common when you have cyclical phenomena like time. Space can also be cyclical, like when Pac-Man goes off the right edge of the screen only to come back around on the left edge or when you turn a combination lock.
You can solve wrapped addition problems by envisioning the cycle on a clock. In fact, you may have heard wrapped addition and subtraction called clock arithmetic. Here’s a clock for a cycle of size 8:
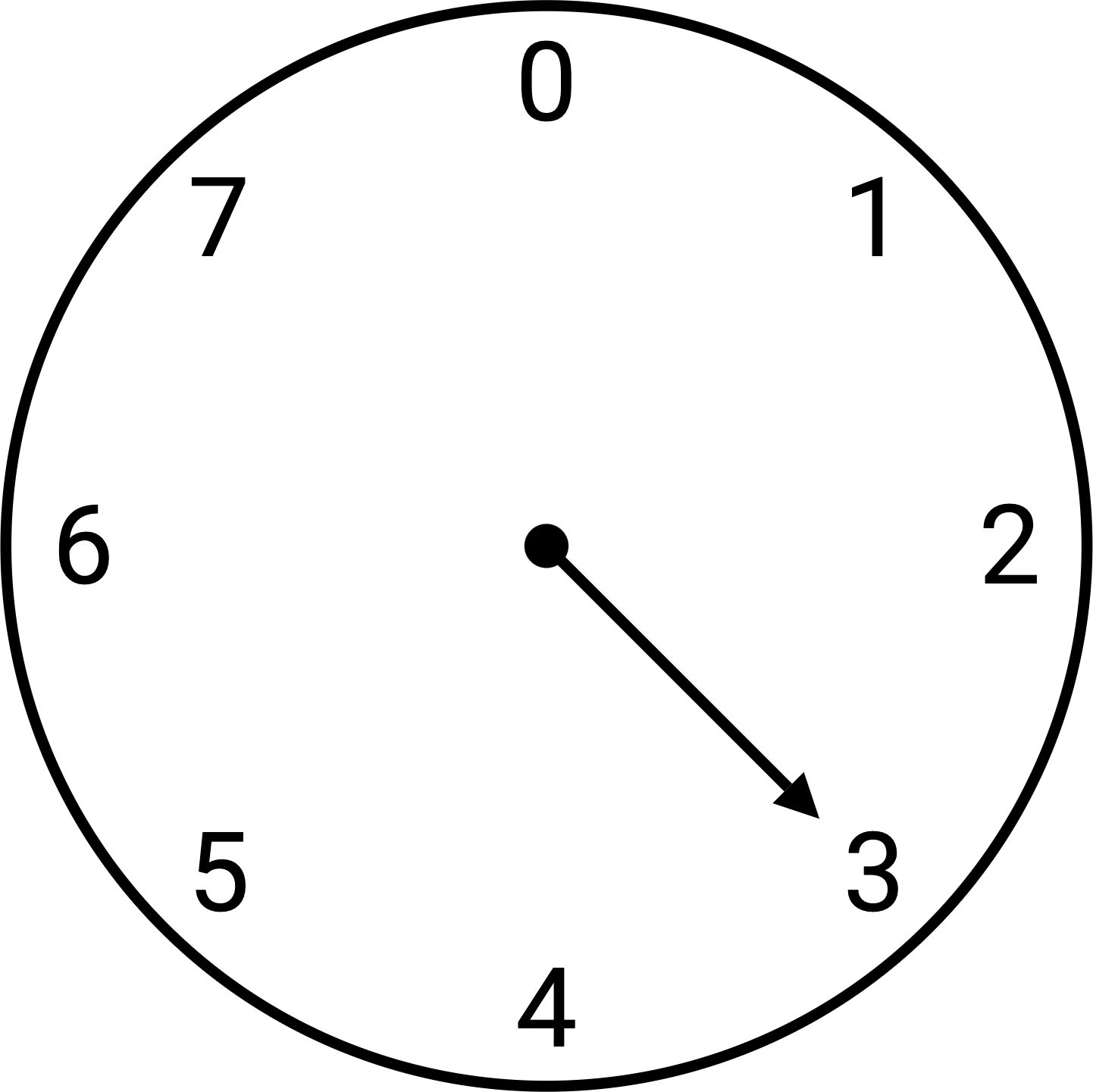
Notice how the numbers run 0 through 7. When you start at 0 instead of 1, the maximum is one less than the size. Currently the clock reads 3. If we advance 11 ticks around the clock, we land at 6.
One way to solve wrapped addition problems is to compute the remainder of this expression:
For our example, we have 3 + 11, which is 14. When we divide 14 by the size 8, we find that only one 8 can fit in, leaving a remainder of 6. And that’s the answer we want.
Many programming languages have an operator for computing this remainder. It’s called the mod operator and is often notated as %. To perform a wrapped addition, we write an expression like this:
wrapped = (current + advance) % size
We’ll be using wrapped addition to generate many shapes. We’ll start at a vertex on the shape’s surface and try to advance by 1 to connect it back up to an earlier vertex.